Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- 아이펠 일기
- 컴파일타임
- 파이썬 주석 변수
- compile time
- AIFFEL 회고
- 파이썬 여러줄 문자열 변수
- 파이썬 긴 문자열 변수
- 파이썬 형변환
- Aiffel
- Linux
- python 문법
- 아이펠 회고
- 런타임
- 파이썬 여러줄 주석
- 모듈 패키지 라이브러리
- 아이펠
- 파이썬 진수변환
- 마크다운 inline 수식
- 마크다운
- 윈도우 커맨드창
- 리눅스
- 마크다운 인라인 수식
- 아이펠일기
- 파이썬 문법
- Python
- 파이썬
- PYTHON 주석 변수
- AIFFEL 일기
- AIFFEL일기
- Markdown
Archives
- Today
- Total
튜토리얼에도 고난과 역경이 있다.
데이터 전처리) 이상치란? Outlier? 본문
728x90
이상치 Outlier란?
대부분의 값의 범위에서 벗어나 극단적으로 크거나 작은 값. 즉, 노이즈 같은것!
이상치를 찾는 방법
1. z score
가장 많이 쓰는 방법으로 평균과 표준 편차를 이용한다.
-> z score : 평균을 빼주고 표준 편차로 나누는 방법

- μ : 평균
- σ : 표준 편차
코드상의 구현
abs(df[col] - np.mean(df[col])): 데이터 - 평균 의 절대값abs(df[col] - np.mean(df[col]))/np.std(df[col]): 표준편차로 나눠줌df[abs(df[col] - np.mean(df[col]))/np.std(df[col])>z].index: 값이 z보다 큰 데이터 인덱스 추출
2. Modified Z-score method
http://colingorrie.github.io/outlier-detection.html
3. 사분위 범위수 IQR method
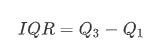
과 같이 제 3사분위 수에서 제 1사분위 값을 뺀 값으로 데이터의 중간 50% 범위라고 생각하면 된다.
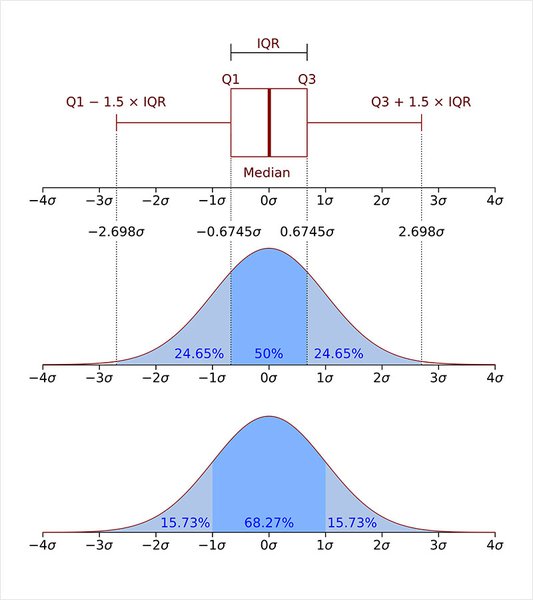
Q1 - 1.5 * IQR보다 왼쪽에 있거나 Q3 + 1.5 * IQR보다 오른쪽에 있는 경우 이상치라고 판단한다.
다음은, 이해를 돕기 위한 그림이다.
z-score 방법이 가지는 단점 2가지
1) Robust하지 못하다 - 왜나하면 평균과 표준편차 자체가 이상치의 존재에 크게 영향을 받기 때문이다.
2) 작은 데이터셋의 경우 z-score의 방법으로 이상치를 알아내기 어렵다. 특히 item이 12개 이하인 데이터셋에서는 불가능하다.
출처
- AIFFEL LMS
반응형
'나의 공부 > 인공지능' 카테고리의 다른 글
| [fd_18] 딥러닝 들여다보기 (0) | 2022.01.22 |
|---|---|
| [fd_16] 파이썬으로 이미지 다루기 (0) | 2022.01.20 |
| 데이터 전처리의 다양한 기법 (0) | 2022.01.19 |
| 강화학습 ) 1강. Introdution to Reinforcement Learning (0) | 2022.01.12 |
| 데이터 전처리) 결측치 처리 방법 (0) | 2022.01.03 |


